Advent of code 2023 - Day 3: Gear Ratios

2023-12-18

Python

Table of Contents

This year I try to record my attempt at solving the Advent of Code 2023 riddles. This is Day 3 - see https:adventofcode.com/2023/day/3

Part 1 #

Lets first read the task:

The engine schematic (your puzzle input) consists of a visual representation of the engine. There are lots of numbers and symbols you don’t really understand, but apparently any number adjacent to a symbol, even diagonally, is a “part number” and should be included in your sum. (Periods (.) do not count as a symbol.)

Here is an example engine schematic:

467..114..
...*......
..35..633.
......#...
617*......
.....+.58.
..592.....
......755.
...$.*....
.664.598..

In this schematic, two numbers are not part numbers because they are not adjacent to a symbol: 114 (top right) and 58 (middle right). Every other number is adjacent to a symbol and so is a part number; their sum is 4361.

Of course, the actual engine schematic is much larger. What is the sum of all of the part numbers in the engine schematic?

My input file: 2023-12-03-1-aoc.txt

Okay, let’s first get the input as a numpy character array

import numpy as np
import pandas as pd
import sys
import matplotlib.pyplot as plt
from scipy import ndimage as ndi
np.set_printoptions(threshold=sys.maxsize)

txt = pd.read_table('data/2023-12-03-1-aoc.txt', names=['code'])
arr = np.chararray((txt.size, txt.size), unicode=True)

txt['code'] = txt.loc[:, 'code'].apply(lambda x: [i for i in x])

for i, code in enumerate(txt['code']):
    arr[i, :] = code

print((arr[:15, :15]))

[['.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.']
 ['.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '5' '3' '.' '4']
 ['.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '*' '.' '.' '.' '.']
 ['.' '.' '.' '.' '.' '.' '.' '7' '2' '6' '.' '.' '.' '.' '.']
 ['.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '9' '5']
 ['.' '.' '.' '.' '.' '.' '.' '7' '3' '8' '.' '.' '.' '*' '.']
 ['.' '7' '4' '.' '.' '.' '.' '.' '.' '.' '.' '.' '3' '6' '6']
 ['.' '.' '.' '*' '1' '2' '6' '.' '.' '.' '.' '.' '.' '.' '.']
 ['.' '.' '.' '.' '.' '.' '.' '.' '3' '3' '1' '/' '.' '.' '9']
 ['.' '.' '.' '.' '/' '.' '.' '.' '.' '.' '.' '.' '.' '.' '*']
 ['.' '.' '.' '.' '9' '5' '3' '.' '.' '.' '.' '3' '5' '5' '.']
 ['.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.']
 ['.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.' '.']
 ['.' '6' '8' '5' '.' '.' '.' '.' '*' '.' '.' '.' '.' '7' '0']
 ['.' '.' '.' '.' '.' '.' '.' '.' '.' '9' '3' '8' '.' '.' '*']]
/tmp/ipykernel_18336/87086526.py:9: DeprecationWarning: `np.chararray` is deprecated and will be removed from the main namespace in the future. Use an array with a string or bytes dtype instead.
  arr = np.chararray((txt.size, txt.size), unicode=True)

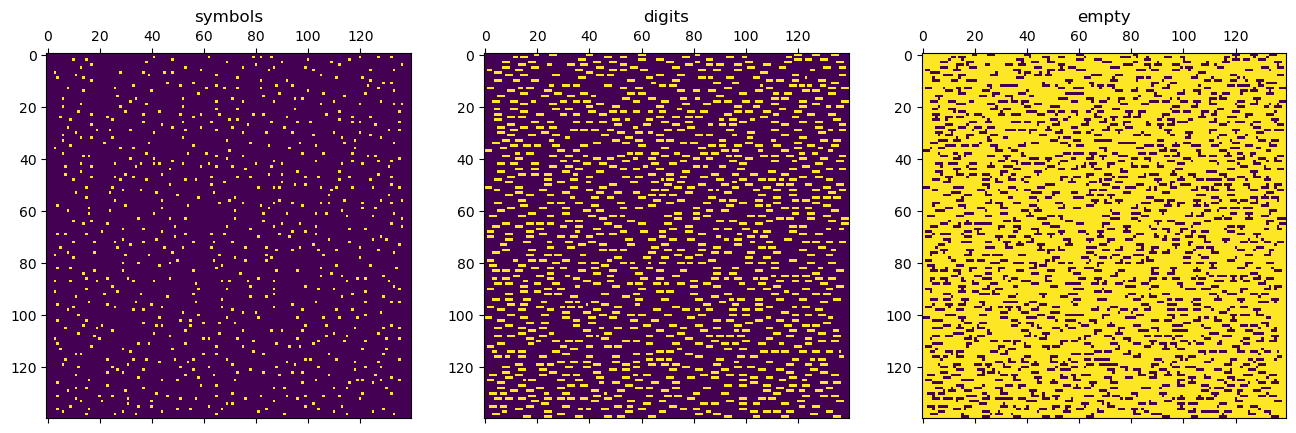
Now extract symbols, digits and the empty space. We use the numpy character methods for that. This way, we create a binary mask for all digits and a binary mask for all empty space (.). The symbols are then every character which is neither.

digits = np.char.isdigit(arr)
empty = np.char.endswith(arr, '.')
symbols = ~(digits | empty)

# just for visualization
plt.figure(figsize=(16, 5))
plt.subplot(131, title='symbols').matshow(symbols)
plt.subplot(132, title='digits').matshow(digits)
plt.subplot(133, title='empty').matshow(empty)
plt.show()

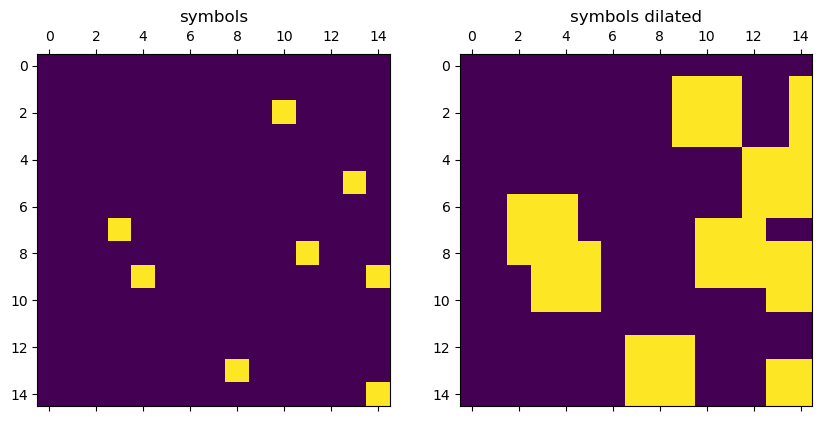
Now we use the image processing technique of dilation on the symbols mask. So that we get a new mask which covers the surroundings of all symbols. We use this afterwards to check if the digits are near a symbol.

struct = ((1, 1, 1), (1, 1, 1), (1, 1, 1))
dilate = ndi.binary_dilation(symbols, structure=struct)
plt.figure(figsize=(10, 6))
plt.subplot(121, title='symbols').matshow(symbols[:15, :15])
plt.subplot(122, title='symbols dilated').matshow(dilate[:15, :15])
plt.show()

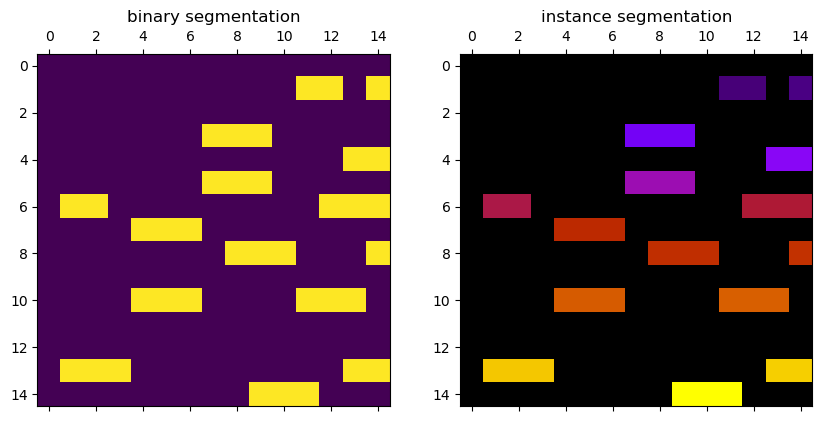
Creating this masks as before could be understood as a binary segmentation, as each element in our mask is either True or False. To extract the single digits, we’ll convert the binary digits segmentation into a instance segmentation, where each connected segment has an own index.

markers, num_features = ndi.label(digits)
plt.figure(figsize=(10, 6))
plt.subplot(121, title='binary segmentation').matshow(
    digits[:15, :15])
plt.subplot(122, title='instance segmentation').matshow(
    markers[:15, :15], cmap='gnuplot')
plt.show()

Now, for each instance, we check if the dilated binary mask overlaps with the instance and if yes, we extract the number.

numbers = [int(''.join(arr[markers == i]))
           for i in range(1, num_features+1)
           if np.any((markers == i) & dilate)]

Then, we just sum up:

sum(numbers)

Part 2 #

Let’s first read the second task!

The missing part wasn’t the only issue - one of the gears in the engine is wrong. A gear is any * symbol that is adjacent to exactly two part numbers. Its gear ratio is the result of multiplying those two numbers together.

This time, you need to find the gear ratio of every gear and add them all up so that the engineer can figure out which gear needs to be replaced.

Consider the same engine schematic again:The missing part wasn’t the only issue - one of the gears in the engine is wrong. A gear is any * symbol that is adjacent to exactly two part numbers. Its gear ratio is the result of multiplying those two numbers together.

This time, you need to find the gear ratio of every gear and add them all up so that the engineer can figure out which gear needs to be replaced.

Consider the same engine schematic again:

467..114..
...*......
..35..633.
......#...
617*......
.....+.58.
..592.....
......755.
...$.*....
.664.598..

In this schematic, there are two gears. The first is in the top left; it has part numbers 467 and 35, so its gear ratio is 16345. The second gear is in the lower right; its gear ratio is 451490. (The * adjacent to 617 is not a gear because it is only adjacent to one part number.) Adding up all of the gear ratios produces 467835.

What is the sum of all of the gear ratios in your engine schematic?

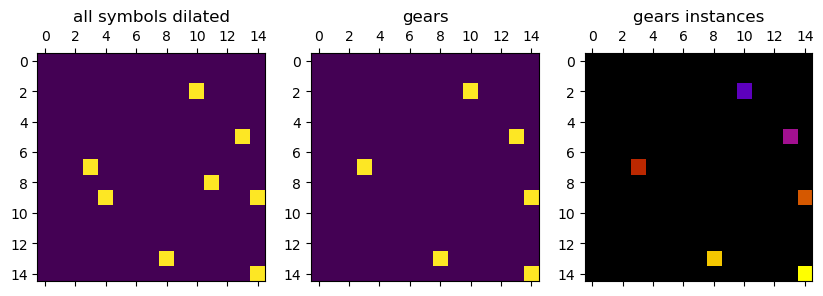
We’ll use the same method as before, but this time only extract * and create the instance segmentation before the dilation. Why? Because when we dilate first, we could merge two independent gears into one instance.

gear = np.char.endswith(arr, '*')
gear_markers, gear_num = ndi.label(gear)

plt.figure(figsize=(10, 6))
plt.subplot(131, title='all symbols dilated').matshow(
    symbols[:15, :15])
plt.subplot(132, title='gears').matshow(
    gear[:15, :15])
plt.subplot(133, title='gears instances').matshow(
    gear_markers[:15, :15], cmap='gnuplot')
plt.show()

Now, we step through each gear instance, create a mask for that gear, dilate it, and then step through all digits and check if they are in the gear mask. If we get two digits in the end, we multiply them to get the gear ratio and save the ratios to a list.

gear_ratios = []
for i in range(1, gear_num+1):
    gear_binary = gear_markers == i
    gear_dil = ndi.binary_dilation(gear_binary, structure=struct)
    part_numbers = [int(''.join(arr[markers == j]))
                    for j in range(1, num_features+1)
                    if np.any((markers == j) & gear_dil)]
    if len(part_numbers) == 2:
        gear_ratios.append(part_numbers[0] * part_numbers[1])

Now, we just sum the output again:

sum(gear_ratios)

79026871